Escoamento externo e convecção natural e forçada

Escoamento externo, convecção natural e forçada

Tipos de escoamento

O escoamento pode ser classificado em dois tipos:

1. Escoamento externo: não é confinado por paredes;
2. Escoamento interno: é confinado por paredes.

Por exemplo, o escoamento externo seria característico do fluxo de ar ao redor de um veículo em movimento, enquanto que o escoamento interno ocorreria, por exemplo, dentro de uma tubulação industrial.

Escoamento laminar x turbulento

Ademais, a natureza do escoamento também pode ser classificada entre laminar ou turbulenta. Um escoamento laminar apresenta um fluxo previsível e com aparência vitrificada, enquanto que o turbulento ocorre de maneira caótica e imprevisível.

Diferença entre fluxo laminar e turbulento

Além do aspecto visual, a própria natureza dos fluxos laminar e turbulento geram outras variações. Por exemplo, no escoamento laminar, as partículas tendem a se agregar em camadas, com pouca mistura – enquanto que o oposto ocorre para o escoamento turbulento – no qual a mistura entre partículas é frequente e imprevisível. Diferenças como essas afetam, por exemplo, a energia necessária para bombear os fluidos, e até mesmo a aerodinâmica.

Lei de Newton da viscosidade

A princípio, antes de discutir a lei de Newton da viscosidade, é necessário destacar uma condição importante dos fluidos: a lei de não-deslizamento (no-slip). Ela indica que, para o fluido em contato direto com uma superfície, a partícula imediatamente em contato se moverá na mesma velocidade da superfície (estará parada caso a superfície esteja imóvel) – isto é, o fluido é aderido à superfície.

Tensão de cisalhamento

Uma medida utilizada para aferir a viscosidade de fluidos é o comportamento perante uma tensão de cisalhamento. A tensão de cisalhamento é uma força deformadora aplicada paralelamente ao fluido, que, em conjunto com a característica de no-slip, permite a classificação de diferentes materiais.

Fluidos que apresentam tensão de cisalhamento proporcional à taxa de deformação são chamados de fluidos newtonianos, em oposição aos fluidos não-newtonianos, que podem variar irregularmente neste quesito.

Assim, fluidos newtonianos são modelados pela equação:

\[\tau\propto\frac{d\alpha}{dt}\]

E a Lei de Newton da viscosidade, propriamente, é representada pela equação:

\[\tau=\mu\frac{dv}{dy}\]

Tal que:

• \(\frac{dv}{dy}\) indica o gradiente de velocidade;
• \(\mu\) indica a viscosidade absoluta (ou dinâmica) do fluido.

Fluidos não-newtonianos

O nome é pouco utilizado diariamente, mas fluidos não-newtonianos são comumente utilizados. Uma lista deles inclui:

• Creme dental;
• Algumas tintas;
• Ketchup.

Camada limite

Tendo em mente os conceitos de viscosidade e escoamento, para um fluido próximo a uma superfície, a camada limite é o nome dado para a região na qual o fluido escoa com até 99% da velocidade original.

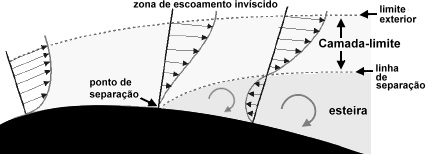Representação da camada limite

Essa região é interessante pois o fluido em contato com o material deve apresentar velocidade nula (no-slip), afetando as partículas imediatamente próximas pelas tensões de cisalhamento (forças paralelas).

Nota-se que a espessura da camada limite tende a aumentar a medida que o fluido se desloca próximo a camada plana, devido à acentuação dos efeitos de viscosidade e tensões de cisalhamento.

Esses efeitos são importantes para determinar, por exemplo, o coeficiente de atrito local para escoamentos externos:

\[C*f\equiv\frac{2\tau_s}{\rho{}v^2*\infty}\]

Regiões da camada limite

A camada limite pode ser subdividida em três regiões, para uma superfície suficientemente extensa:

• Laminar;
• Transição;
• Turbulenta.

Camada limite laminar

Na camada limite laminar, o movimento do fluido é extremamente ordenado, e podem ser identificadas com clareza linhas de corrente nas quais as partículas se movimentam. As componentes de velocidade são nas direções x e y.

Camada limite de transição

Na transição, há a passagem de uma camada limite laminar para uma turbulenta. O comportamento não é estritamente caótico, nem ordenado como na camada laminar.

Camada limite turbulenta

Por sua vez, na camada turbulenta, o comportamento é altamente irregular. Há rápida mistura no interior da camada limite, e o movimento é tridimensional e aleatório.

Devido a essas misturas, o perfil de velocidade na camada turbulenta tende a ser menor do que na camada laminar, pela dissipação das componentes da velocidade.

Número de Reynolds

Para determinar se uma camada é laminar ou turbulenta, o número adimensional de Reynolds correlaciona os termos inerciais aos termos viscosos. Isto é:

\[Re=\frac{\rho{}UL}{\mu}=\frac{\text{Termos inerciais}}{\text{Termos viscosos}}\]

Tal que:

• Força inercial = massa x aceleração;
• Força viscosa - tensão superficial x área.

Assim, o número de Reynolds para determinada região pode ser calculado através de:

\[Re*x=\frac{\rho{}\cdot{}v*\infty{}\cdot{}x}{\mu}=\frac{v\_\infty{}\cdot{}x}{\upsilon}\]

Seja:

• \(\rho=\) densidade do fluido;
• \(\mu=\) viscosidade dinâmica do fluido;
• \(\upsilon=\) viscosidade cinemática do fluido;
• \(v_\infty=\) velocidade do fluido na corrente livre;
• \(x=\) comprimento característico.

Em suma:

• Baixos valores de Reynolds indicam um escoamento laminar;
• Valores elevados de Reynolds indicam um escoamento turbulento.

A transição entre laminar e turbulento é definida como para \(Re_x=5\cdot{}10^5\)

Camada limite térmica

Similarmente a camada limite de escoamento, a camada térmica indica a região na qual se desenvolvem gradientes de temperatura quando o fluido apresenta uma temperatura diferente da placa.

Para isso, considera-se que as partículas do fluido que entram em contato direto com a superfície da placa imediatamente atingem a temperatura da placa. E que as partículas com temperatura alterada propagam essa transferência às partículas próximas, formando um gradiente.

A espessura da camada limite térmica pode ser definida pela distância da superfície na qual a temperatura do fluido é ao menos 99% a temperatura da placa.

Número de Prandtl

Dadas as duas camadas limites exploradas – hidrodinâmica e térmica – define-se o número de Prandtl para relacionar as duas camadas, tal que:

\[Pr=\frac{\text{Difusão de quantidade de movimento}}{\text{Difusão de energia}}\]