Mecanismos de transferência de calor

Módulo 3 – Transferência de calor: Condução, Convecção e Radiação

A transferência de calor é um fenômeno que ocorre naturalmente sempre que há diferença de temperatura entre um ou mais meios. Por fim de classificação, a transferência de calor pode ocorrer através de três modos: condução, convecção e radiação.

Modos de transferência de calor

Em uma visão geral, os modos de transferência de calor podem ser rudimentariamente descritos como:

1. Condução: Transferência de calor através do contato de partículas de dois meios estacionários.
2. Convecção: Transferência de calor através do contato de partículas em ao menos um meio em movimento.
3. Radiação: Transferência de calor através da emissão de ondas eletromagnéticas.

Condução: mecanismo físico

A transferência ocorre através da colisão de partículas mais energéticas com partículas menos energéticas, transferindo momento no instante de contato.

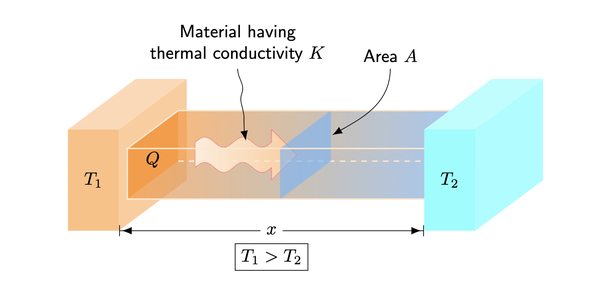Transferência de calor através de condução

Convecção: condução e advecção

A primeira etapa da convecção faz uso do mesmo mecanismo de transferência de calor da condução, isto é, a colisão entre partículas com maior energia a partículas com menor energia. Já a segunda etapa, dado que há movimento de partículas, as partículas aquecidas tendem a ‘flutuar’ através do aumento da força de empuxo pelo aquecimento, trocando de posição com partículas menos quentes. Esse ciclo de advecção implica em uma maior transferência de calor.

Convecção forçada e natural

Ademais, a convecção pode ser natural, ou seja, surgir em virtude da própria transferência de calor, como explicada pela advecção via aquecimento natural. Dito isso, a convecção pode ser estimulada forçadamente, por exemplo, ao introduzir um ventilador a um trocador de calor.

Transferência de calor através de convecção forçada e natural

Nomenclaturas

• $ q $ – Calor [J]
• $ \dot{q} $ – Taxa de transferência de calor [$W$]
• $ \dot{q}’ $ – Potência linear [$\frac{W}{m}$]
• $ \dot{q}’’ $ – Fluxo de calor [$\frac{W}{m^2}$]
• $ \dot{q}’’’ $ – Densidade de potência [$\frac{W}{m^3}$]

Lei de Fourier

• \(\large\dot{q}\_{x} = -kA\frac{\partial{T}}{\partial{x}}\)
• \(\large\dot{q}_{x}''=\frac{\dot{q}_{x}}{A}=-k\frac{\partial{T}}{\partial{x}}\)

Equação de difusão de calor

\[\large\frac{\partial{}}{\partial{x}}\left(k\frac{\partial{T}}{\partial{x}}\right) + \frac{\partial{}}{\partial{y}}\left(k\frac{\partial{T}}{\partial{y}}\right) + \frac{\partial{}}{\partial{z}}\left(k\frac{\partial{T}}{\partial{z}}\right) + q*{g}''' = \rho{}C*{p}\frac{\partial{T}}{\partial{t}}\]

Condução em parede plana

No cenário onde a condução ocorre de maneira unidirecional, pode-se reduzir a equação de difusão de calor para: \(\frac{\partial{}}{\partial{x}}\left(k\frac{\partial{T}}{\partial{x}}\right)=0\). Como \(\dot{q}_x''=-k\frac{\partial{T}}{\partial{x}}\), logo \(\frac{\partial{q''}}{\partial{x}}=0\). Então, \(\dot{q}_x''\) ou \(-k\frac{\partial{T}}{\partial{x}}\) é constante.

Integrando a equação obtida anteriormente em x, obtêm-se:

• \(\int{-k\frac{\partial{T}}{\partial{x}}dx}=\int{Cdx}\)
• \(T(x)=C_{1}x+C_{2}\)

Assim, nota-se que a temperatura varia de acordo com a distância percorrida dentro da parede unidimensional, em função de x (distância).

Condução em parede unidimensional

Equação: temperatura total em função da distância

Tal que, de forma ingênua, pode-se deduzir uma equação simplificada para a transferência de calor via parede unidimensional:

\[\large{}T(x)=(T*{2}-T*{1})\frac{x}{L}+T\_{1}\]

Essa equação, todavia, prevê uso em condições específicas, como:

1. Condução unidimensional;
2. Regime estacionário;
3. Parede plana;
4. Sem geração de calor;
5. Condutividade térmica (k) constante.

Neste caso, espera-se que a transferência de calor deva comportar-se linearmente conforme x se aproxima de L.

Equação: transferência de temperatura por condução

Ignorando o coeficiente linear na equação para determinar a temperatura total, pode-se especificar a modelagem da equação de transporte:

\[\large{}q*{x}=-kA\frac{dT}{dx}\approx{}kA\frac{T*{1}-T\_{2}}{L}\]

No mesmo sentido, pode ser modelada a equação de fluxo de calor a partir da equação da taxa de transferência:

\[\large{}q*{x}''=\frac{q*{x}}{A}\approx{}k\frac{T*{1}-T*{2}}{L}\]

Analogia com circuitos elétricos

Assim como na lei de OHM, pode-se fazer uma relação similar entre a taxa de transferência de calor, a diferença de temperaturas e a resistência térmica. De tal forma, que muitos problemas podem ser simplificados ao montar um ‘circuito térmico’, que permite juntar resistências térmicas de diferentes materiais em uma conta unificada.

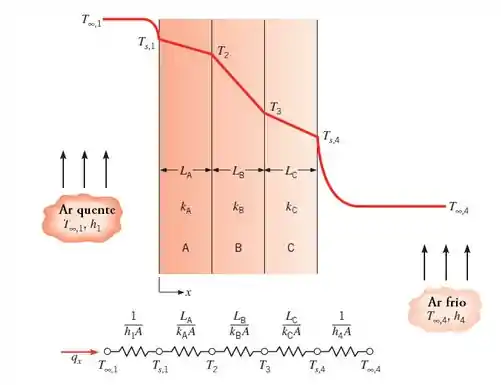Analogia de circuito térmico com circuito elétrico

Isolando na equação de transferência, pode-se obter as resistências:

• Resistência à condução: \(R_{condução}=\frac{L}{kA}\)
• Resistência à convecção: \(R_{convecção}=\frac{1}{hA}\)
• Resistência à radiação: \(R_{radiação}=\frac{1}{h_{r}A}\)

Sistemas radiais

O estudo de sistemas radiais é muito interessante, por exemplo, para a modelagem da transferência de calor em dutos e maquinários. A lei de Fourier pode ser modificada para coordenadas cilíndricas com esse objetivo:

\[\large\frac{1}{r}\frac{\partial{}}{\partial{r}}\left(kr\frac{\partial{T}}{\partial{r}}\right) + \frac{1}{r^2}\frac{\partial{}}{\partial{\phi}}\left(k\frac{\partial{T}}{\partial{\phi}}\right) + \frac{\partial{}}{\partial{z}}\left(k\frac{\partial{T}}{\partial{z}}\right) + q*{g}''' = \rho{}C*{p}\frac{\partial{T}}{\partial{t}}\]

Aplicando as mesmas simplificações, pode-se definir equação em função do raio, simplificando-a para problemas mais simples. Nesse caso, nota-se igualmente que um dos fatores deve ser constante para comportar as derivações.

\[\large{}kr\frac{dT}{dr}=cte\]

Assim, obtêm se a família de soluções:

\[\large{}T(r)=C*{1}\left(\ln{r}\right)+C*{2}\]

De tal forma que a resistência térmica pode ser definida como, para um cilindro oco, por exemplo:

\[\Large{}R\_{t,condução}=\frac{\ln{}\left(\frac{r_2}{r_1}\right)}{2k\pi{}L}\]

Sistema radial com paredes compostas

Formulação concentrada

A formulação concentrada é um método que permite que se calcule a transferência de calor entre um sólido e o ambiente em função do tempo ao aproximar o seu gradiente de temperaturas internas como uniforme, tal que indica a resolução de tais problemas a partir do balanço de energia.

Um exemplo no qual a formulação concentrada (também chamada de capacitância global) pode ser utilizada é para o cálculo de valores relacionados ao resfriamento de um sólido incandescente através do mergulhamento em água a temperatura ambiente, muito comum durante o endurecimento de metais.

Quenching de metal em água

Neste caso, o metal é resfriado através da perda de temperatura, sobretudo por convecção, para o líquido no qual ele é imerso. A troca de calor ocorre até que sua temperatura se iguale à do líquido. Em muitos casos, é possível usar o método de capacitância global caso o coeficiente de transferência de calor do material seja alto, uma vez que a aproximação da formulação concentrada consistem em tomar \(k\to\infty{}\). Ou seja, o calor dissipado para convecção para o líquido se equilibra rapidamente na superfície interna do material.

Com essas considerações, obtemos a equação:

\[\frac{T-T_{\infty}}{T_0-T_{\infty}}=\exp{\left[-\left(\frac{h\cdot{}A_s}{\rho{}\cdot{}V\cdot{}C}\right)\cdot{}t\right]}\]

Tal que:

• \(T\) é a temperatura final do sólido (°C);
• \(T_0\) é a temperatura inicial do sólido (°C);
• \(T_{\infty}\) é a temperatura constante do líquido (°C);
• \(h\) é o coeficiente de transferência de calor do líquido por convecção (\(\frac{W}{m^2\cdot{}°C}\));
• \(A_s\) é a área da superfície em contato com o fluido (\(m^2\));
• \(\rho\) é a densidade do sólido (\(\frac{kg}{m^3}\));
• \(V\) é o volume do sólido (\(m^3\));
• \(C\) é o calor específico do sólido (\(\frac{J}{kg\cdot{}°C}\)).

E, manipulando essa equação, a energia total transferida pode ser calculada através de:

\[Q=\rho\cdot{}V\cdot{}C\cdot{}(T_0-T_{\infty})\left[1-\exp{\frac{-t\cdot{}h\cdot{}A_s}{\rho\cdot{}V\cdot{}C}}\right]\]

Por fim, é padronizado que este método pode ser aplicado caso o número adimensional de Biot – que correlaciona a resistência de condução à resistência de convecção – seja menor do que \(0.1\).